اصل اکسترمال 2

ریاضی دان ورزیده مجهز به یک سری اصول و فنون با دامنه کاربرد وسیع وساده می باشد که می تواند از آنها در حالت های مختلف استفاده نمایید. این اصول و فنون وابسته به موضوعی ویژه نبوده و در کلیه شاخه های ریاضی قابلیت استفاده را دارند. ریاضی دان به این اصول فکر نمی کند بلکه به طور ناخودآگاه از آن مطلع می باشد

 به اصل های زیر دقت کنید:

الف.هر زیر مجموعه محدود  از اعداد صحیح یا حقیقی دارای یک عنصر مینیمم و یک عنصر ماکسیمم است . (اصل اکسترمال)
ب.هر زیرمجموعه غیر تهی از اعداد صحیح مثبت دارای کوچک ترین عضو است. این را « اصل خوش ترتیبی» می نامند . (حالت کلی تر اصل اکسترمال)
ج.مجموعه نامحدود از اعداد حقیقی ضرورتاً دارای عضو ماکسیمال یا مینیمال نیست. اگر از بالا کران دار باشد، آنگاه دارای کوچک ترین کران بالاست که آن را سوپریمم می نامیم. اگر از پایین کران دار باشد دارای بزرگترین کران پایین است و آن را اینفیمم می نامیم. (کلی تر از اصل خوش ترتیبی)

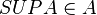و هم چنین  اگر  باشد آنگاه و اگر 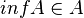 آنگاه .

در استفاده از اکسترمال سعی می کنیم وجود یک حالت را به اثبات برسانیم. اصل اکسترمال به ما می گوید که با انتخاب این حالت سعی کنید برخی حالت های ماکزیمم و مینیمم آن را بررسی کنید. حالت حاصل نشان دهنده تقریبی وضعیت خواسته شده است هر چند کاملاً با آن منطبق نمی نماید ولی با کمی تغییر روی توابع به حالت اصلی می توان رسید. اگر راه های مختلفی برای بهینه سازی وجود داشته باشد انتخاب یکی از آنها بسته به نظر ما می باشد. اصل اکسترمال بسیار خلاق است و می تواند الگوریتم روش ساختن آن حالت را به ما نشان دهد. 

چند مسئله:

مثال ۱ : ‏الف. خط حداکثر یک صفحه را به چند بخش تقسیم می کند؟ 

ب. با  صفحه در حالت کلی فضا به چند بخش تقسیم می گردد

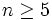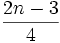مثال 2: ادامه بخش ب: فرض کنیم  نشان دهید در بین  بخش از فضا حداقل  چهاروجهی وجود دارد (). 

مثال 3 (مسئله سیلوستر) :  مجموعه محدود شامل نقاطی از صفحه‌است که هر خط گذرنده ازدو نقطه از نقطه ‏سومی می‌گذرد. ثابت کنید تمام نقاط روی یک خط واقع می‌باشند.‏

مثال 4 : ‏ در کشور اسکانیا هر شهری به شهر دیگر فقط بوسیله یک جاده یک طرفه وصل شده ‏است. ثابت کنید شهری وجود دارد که از هر شهری به آن مستقیم و یا حداکثر به ‏واسطه یک شهر دیگر می‌توان رسید. ‏

منبع: انگل، آرتور. استراتژی‌های حل مسئله، چاپ دوم . تهران: مبتکران ، ۱۳۸۴ 

حل سوال 1 : (به نظر من این مسئله خیلی به اصل اکسترمال ربطی نداره بلکه هدف پیدا کردن اکسترمم است.) الف. یک نفر مبتدی برای حل این مسئله از اینجا شروع می‌کند که . ‏در حقیقت با اضافه کردن یک خط به ‏n‏ خط به سادگی به دست می‌آید که ‏.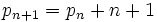

در واقع در این استدلال هیچ اشکالی نیست. چون رابطه بازگشتی پایه و اساس این شوره تفکر است، ‏یک مسئله حل کن تجره گرا ممکن است مسئله را در ذهن خود حل نماید. ما به شماره کردن ‏مسئله می‌پردازیم. یکی از اصول شمارش اساسی تناظر یک به یک برقرار کردن است.‏

اولین سوال این است آیا می‌توان ‏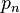 بخش از صفحه را بصورت یک به یک به مجموعه مربوط ‏ساخت که به آسانی بتوان آن را شمرد؟

ترکیب 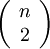 نقطه برخورد ‏n‏ خط را به آسانی می‌توان ‏یافت. اما پایین برخورد دقیقاً در یک بخش وجود دارد (اصل اکسترمال) بنابراین  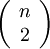بخش را با یک نقطه اشتراک داریم، بخش‌ها بدون نقاط اشتراک در کران پایین ‏واقع نمی‌شود، و بک خط افقی را به ‏n‏+۱ قسمت تقسیم می‌کند .‏ این بخش‌ها را می‌توان بطور منحصر بفرد به این نقطه خط‌ها نسبت داد. بنابراین  یا 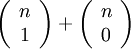 قسمت بدون یک نقطه اشتراک وجود دارد . بنابراین ‏در مجموع داریم:‏

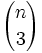ب. سه صفحه یک راس در فضا می سازند. پس  راس وجود دارد که با یک نقطه اشتراک یک بخش از فضا را می سازند. پس  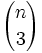بخش با یک نقطه اشتراک پایین داریم هر بخش با یک راس مشترک یک صفحه افقی را به  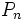قطعه صفحه تقسیم می نماید. بنابراین در بخش های فضا عبارتند از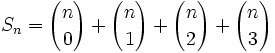 

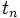حل  سوال 2: بررسی نتیجه مسأله را ساده تر می کند. یک مسأله حل کن با تجربه اغلب با توجه به نتیجه به جستجوی راه حل مسأله می پردازد. فرض کنیم  تعداد چهاروجهی هایی باشد که در  بخش از فضا وجود دارند. پس باید ثابت کنیم که  حدس عددی به ما می گوید که روی  صفحه حداقل دو چهاروجهی وجود دارد. بنابراین این تعداد باید بر 4 بخش پذیر باشد. با توجه به استدلال فوق به راحتی می توان راه حل مسأله را یافت. فرض کنیم 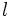 یکی از  صفحه باشد. این صفحه فضا را به دو نیم فضای  و 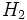 تقسیم می نماید. حداقل یکی از نیم فضاها مثلاً  شامل راس های می باشد. 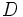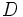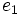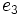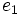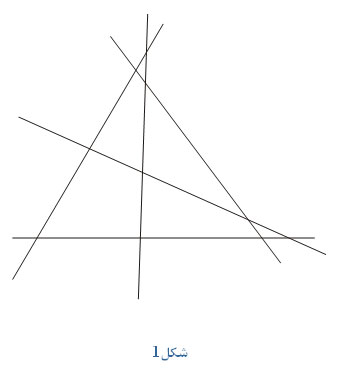در  ما راس  را کمترین فاصله نسبت به  در نظر می گیریم (اصل اکسترمال)  فصل مشترک صفحات  ،  و  می باشد و بنابراین  ،  ،  و 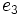 یک چهاروجهی مانند  تعریف می کند به شکل مقابل.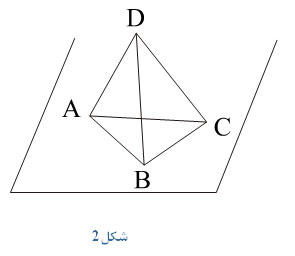 

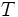هیچ یک از  صفحه باقی مانده با  تقاطع ندارد. بنابراین  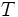یکی از بخش ها بوده که به وسیله  صفحه به وجود آمده است. اگر صفحه ای مانند 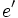 چهاروجهی  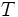را قطع نماید، بنابراینe' باید یکی از یال های  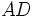، و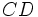 را در نقطه ای مانند  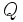قطع نماید که فاصله کمتری از  تا 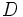 دارد و این تناقض است. 
مطلب فوق برای هر  صفحه صادق است. حال اگر رئوس در هر دو طرف یک صفحه باشند، پس حداقل دو چهاروجهی به وجود می آیند. حال کافی است نشان دهیم در این  صفحه سه چهاروجهی وجود دارد که تمام رئوس آن در یک طرف صفحه واقع می باشند. 
این مطلب را با مثال نقیض ثابت می کنیم. فرض کنیم چهار صفحه 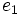 ،  ،  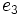و  وجود داشته باشد. آنها چهاروجهی را ناحیه بندی می کنند. شکل زیر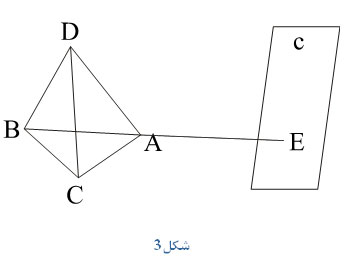 

این صفحه نمی تواند هر شش یال چهاروجهی را قطع نماید. فرض کنیم امتداد را در نقطه 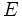 قطع نماید. پس  و 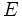 در دو طرف مختلف صفحه  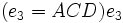واقع می شود که یک تناقض است. 

حل سوال 3 : ‏ (این مسئله به وسیله سیلوستر در سال ۱۸۹۳ طرح شد و در سال ‏‏۱۹۳۳ توسط گالی به روش پیچیده‌ای حل گردید و سپس در سال ۱۹۴۸ درچند خط با ‏اصل اکسترمال توسط کلی حل گردیده‌است.‏) فرض کنیم این نقاط هم خط نیستند. زوج (‏P,L‏ ‏‎(‎‏ عبارت است از خطی مانند‏ و نقطه‌ای مانند ‏ غیر واقع بر ‏‏. حال نقطه‌ای را در نطر می‌گیریم که فاصله اش ‏از خط می‌نیمم باشد. فرض کنیم ‏ پای عمودی است که از نقطه  بر خط‏‏‏ وارد ‏شده‌است. بنابراین بنا به فرض حداقل سه نقطه ‏‏ بر خط قرار دارد. فرض ‏کنیم دو نقطه ‏‏ و‏‏ در یک طرف ‏‏ واقع باشند.‏ و فرض کنیم ‏b‏ به‏f‎‏ تا‏a‎‏ نزدیکتر باشد آنگاه فاصله ‏b‏ تا‏‎‏ ‏ap‏ کمتر از ‏d‏ می‌باشد و ‏این تناقض است . ‏

حل سوال4 :‏ فرض کنیم  حداکثر جاده‌های منتهی به یک شهر باشد. و فرض کنیم ‏‏ شهری ‏باشد که حداکثر جاده‌ها به آن وصل شده باشد. فرض کنیم ‏ مجموعه شهری ‏باشد که به  متصل هستند و فرض کنیم ‏‏ مجموعه تمام شهرهای نامتصل به ‏‏ ‏و موجود در ‏ باشد. ‏

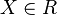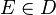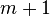اگر ‏R‏ تهی باشد حکم ثابت است. اگر ‏ ‏ باشد شهری مانند  وجود دارد که ‏از طریق آن می‌توان به ‏M‏ رسید یعنی X → M → E. اگر چنین ‏‏ وجود نداشته باشد، پس به شهر‏ می‌توان از طریق شهرهای‏‎‏ ‏و از  رسید. بنابراین ‏ جاده به  منتهی می‌شود که یک تناقض نسبت به ‏فرض در مورد  است. بنابراین به هر شهر به طور حداکثر به حالت حکم مسئله ‏می‌توان رسید.‏